pKa calculation
This background material explains the theory behind the pKa calculation:
Introduction
Chemical properties of molecules depend largely on whether they are ionized or not. Most organic molecules are capable of gaining and/or losing a proton in aqueous solutions. Proton transfer most frequently occurs between water and any ionizable atom of the organic molecule.
The molecule's response to protonation or deprotonation depends significantly on the site that was disturbed by proton transfer. Partial charge distribution in the molecule also varies with protonation of the acid/base active sites. Since the partial charge distribution is very sensitive to the protonation-deprotonation process (both near and far from the disturbed site), it can be used to determine the pKa of a molecule.
Our pKa prediction program is based on the calculation of partial charge of atoms in the molecule.
Acidic and basic molecules are ionized in aqueous solution. Acidic or basic character is assigned to the molecule according to Brönsted's rule. The ratio of the ionized and neutral forms depends on the pH, the temperature and the ion activity of the bulk phase. The ionization constant Ka is obtained from the activity ratio of conjugated base and conjugated acid multiplied with proton activity:
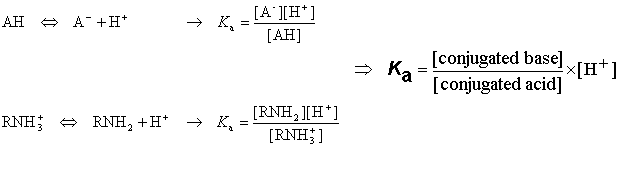
Definition of pK a
The pKa value is obtained from the ionization constant of a molecule using the following definition:
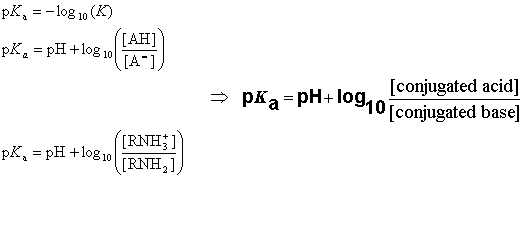
When the pH of the solution is equal with pKa, the concentrations of the dissociated and undissociated species are equal.
Definition of the acidic/basic prefix of p K a
Definition of the basic prefix
Protonated positive ions are considered as protonated basic sites , therefore "basic" prefix is used for them. The neutral basic sites are predefined in the pKa calculator, they also have the "basic" prefix., e.g. if the submitted molecule is CH3NH2 or CH3NH3+,, they get "basic" prefix and pKa=10.08.
Definition of the acidic prefix
Deprotonated negative ions are considered as deprotonated acidic sites , therefore "acidic" prefix is used for them. The neutral acidic sites are predefined in the pKa calculator, they also have "acidic" prefix, e.g. if submitted molecule is CH3COOH or CH3COO- , they get "acidic" prefix and pKa=4.54.
Multiprotic molecules
When a molecule contains more than one ionizable atom, it is called a multiprotic compound. For these types of molecules we need to distinguish between micro and macro acidic dissociation constants. The micro acidic dissociation constant is obtained from the equilibrium concentration of the conjugated acid-base pairs. The macro acidic dissociation constant is obtained from the global mass and charge conservation law. When a molecule has N ionizable sites, the total number of microspecies in the solution is 2N.
Example case
To better understand the difference between micro and macro constants we consider ionization equilibrium of a triprotic acid AH3. Referring to the different deprotonation sites of the AH3 molecule we introduce the upper indexes of the protons:
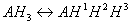
The ionization process of the AH1H2H3 molecule in aqueous solution is described with 12 equilibrium reactions. Microspecies and their charge are summarized in Table 1.

|
Microspecies |
charge |
|
AH1H2H3 |
0 |
|
AH1H2 , AH1H3 , AH2H3 |
-1 |
|
AH1 , AH2 , AH3 |
-2 |
|
A |
-3 |
Tab. 1 Microspecies of AH3 and their charge
The AH3 molecule has three macro acidic constants since it is a triprotic acid. Macro acidic constants K1, K2, and K3 are obtained from the concentration of the microspecies:
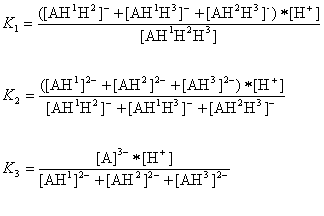
And the three macro pKa values of the AH3 molecule that would be obtained with routine laboratory measurements are as follows:
pKa,1=-log10(K1)
pKa,2=-log10(K2)
pKa,3=-log10(K3)
Examples
The following examples show the different acidic/basic dissociation processes and their related calculations.
Example #1
The ionization steps of p-amino benzoic acid are outlined below. Calculated micro ionization constants k1, k2, k3 and k4 are indicated on the arrows.
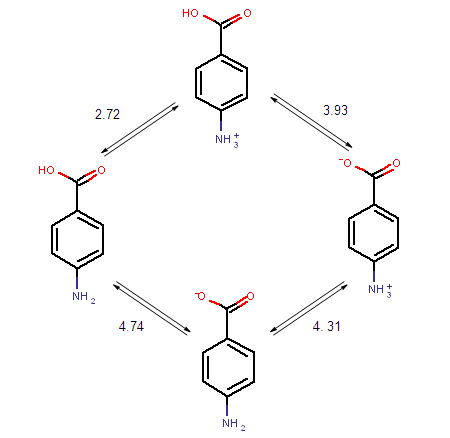
Fig. 1 Ionization steps of p-amino benzoic acid
Below are the calculated and the experimental pKa values of p-amino benzoic acid:
Example #2
Imides and amides can have either acidic or basic character. The extent of amide/imide ionization at a given pH is determined by two acid dissociation constants: pKa,1 is assigned to the deprotonation step RNH 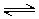 RN- + H+ ;pKa,2 is assigned to the protonation step RNH2+
RN- + H+ ;pKa,2 is assigned to the protonation step RNH2+ 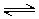 RNH + H+ .
RNH + H+ .
The ratio of anionic and cationic species depends on pKa,1, pKa,2 and the actual pH:
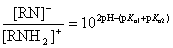
If 2*pH - (pKa,1 + pKa,2) > 0, deprotonation of the amide/imide is favoured, and the molecule is said to have an acidic character.
If 2*pH - (pKa,1 + pKa,2) < 0, protonation of amide/imide is favoured, and it is considered to have a basic character.
Chemists often want to know the ionization state of organic compounds at pH 7.4. (the pH value of human blood) In general, the macro pKas of amide/imide compounds are calculated and their acidic or basic character determined by the above formulas at pH 7.4. We give as an example two amides: phthalamide and 2-pyridone.
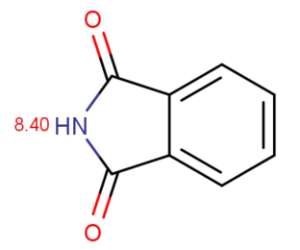

Calculated and measured pKa values of phthalimide and 2-pyridone are given in Table 2.
|
Compound |
Calculated pKa |
Observed pKa |
|
phtalimide |
8.40 |
8.30 |
|
2-pyridone |
11.40 |
11.70 |
Tab. 2 Calculated and measured pKa values of phthalimide and 2-pyridone
Example #3
The value of ionization constants of conjugated acid/base pairs usually falls between 10-2 and 1016, so these limits are generally used to predict the pKa. When an ionizable site in the molecule has an ever weaker basic or acidic character, the ionizable site can be involved in the calculation by increasing the calculation range.
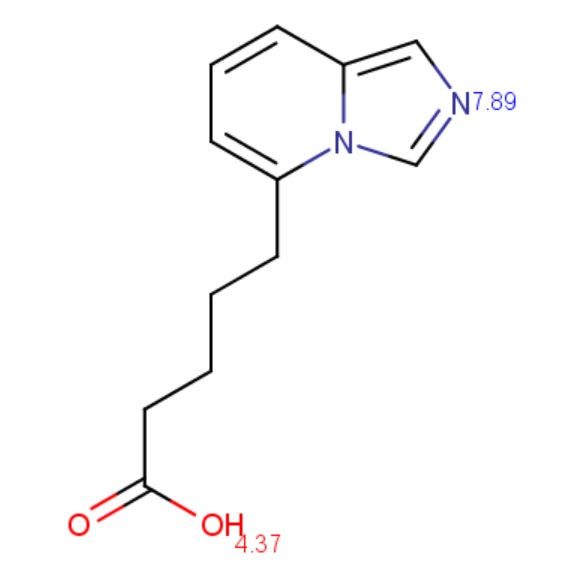
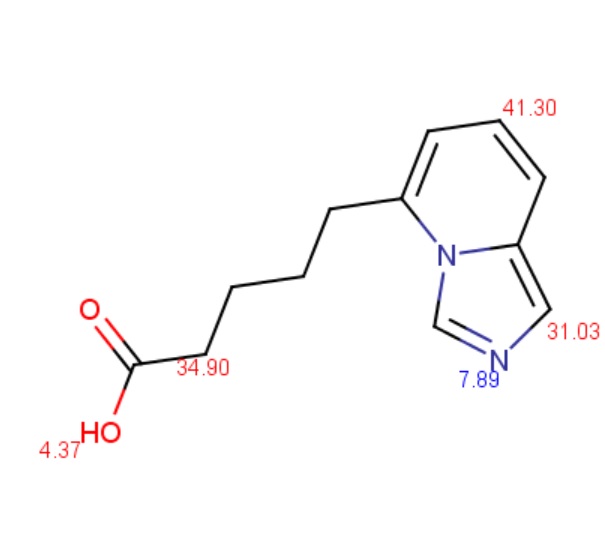
The molecule depicted below contains a very weak acidic N atom. First, macro pKa is calculated with default limits predefined between 10-2 and 1016. Then macro pKa is calculated with altered limits defined between 10-50 and 1050.
Changing the default settings of macro pKa calculation can be done in the Tools > Options > pKa menu of MarvinSketch.
Calculated and observed acidity constants are summarized in Table 3. Measured pKas are taken from Clark et al.
|
pKa |
First calc. |
Second calc. |
Observed |
|
pKa,1 |
4.37 |
4.37 |
4.51 |
|
pKb,1 |
7.89 |
7.89 |
6.01 |
|
pKa,2 |
- |
31.03 |
- |
Table 3. The first three calculated and measured acidity constants
References
-
Prediction of dissociation constant using microconstants, J. Szegezdi and F. Csizmadia, 27th ACS National Meeting, Anaheim, California, March 28-April 1, 2004
-
Calculating pKa values of small and large molecules, J. Szegezdi and F. Csizmadia, American Chemical Society Spring meeting, March 25-29th, 2007
-
Clark, F. H.; Cahoon, N. M., J. Pharm. Sci., 1987, 76, 8, 611-620
-
Dixon, S. L.; Jurs, P. C., J. Comp. Chem., 1993, 14, 12, 1460-1467; doi
-
Csizmadia, F.; Tsantili-Kakoulidou, A.; Panderi, I.; Darvas, F., J. Pharm. Sci., 1997, 86, 7, 865-871; doi
