Evaluator Examples
This page contains detailed examples of using the Chemical Terms Evaluator command line tool:
Introduction
These examples show the application of ChemAxon's Chemical Terms in various ChemAxon products. First we look at some basic examples showing chemical expressions formulated with input read from a molecule context, which applies to the Chemical Terms Evaluator command line tool and chemical expression evaluation and filtering in JChem Cartridge. Next we demonstrate the strength of the chemical terms language in formulating reaction rules, where input is taken from a reaction context. Finally we show how to select search hits by formulating search filters referring to a search context containing the target and query molecules together with the current search hit.
Throughout the examples, use the set of Chemical Terms Reference Tables to look at the function and plugin calculation syntax together with some generic examples.
Prerequisites
To run these examples:
-
The Java Virtual Machine version 1.4 or higher and Marvin / JChem have to be installed on your system.
-
The PATH environment variable have to be set as described in the Installation Guide for Marvin Beans manual.
-
A command shell (under UNIX / Linux: your favorite shell, under Windows: a Cygwin shell or a Command Prompt) has to be run in the evaluator example directory. This do this
under UNIX / Linux type:cd marvin/examples/evaluator
under Windows type:
cd marvin\examples\evaluator
Basic examples
These examples refer to a molecule context and applies the Chemical Terms Evaluator command line tool and chemical expression evaluation and filtering in JChem Cartridge. The working examples below use the evaluate tool but the same expressions can be used in JChem Cartridge as well. However, only boolean expressions (evaluated to true or false) can be used for setting a filtering condition.
Our input molecules are stored in the aroms.smiles fille. The molecules are the following:
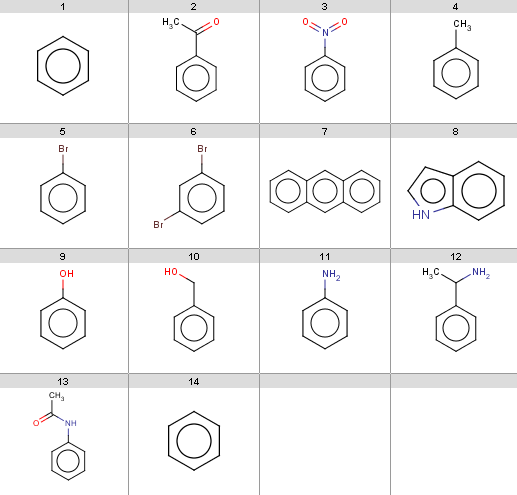
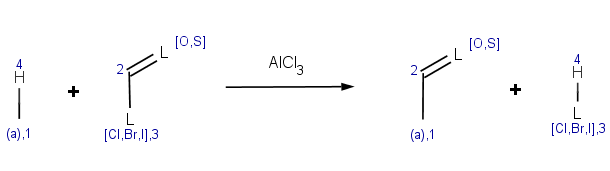
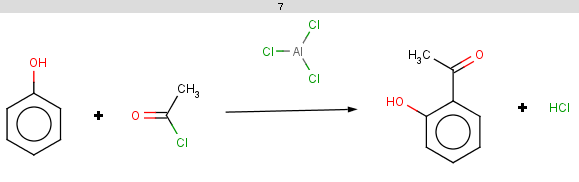
Now we start with some simple plugin calculations and proceed towards the exclude rule of the reaction. The first and last molecules are the same (benzene) because we will react benzene with two different acid-halides when processing the Friedel-Crafts acylation.This will be the first reactant set in the Friedel-Crafts acylation reaction in the Reaction examples section.
Friedel Crafts acylation is the acylation of aromatic rings using an acyl halide in the presence of a strong Lewis acid catalyst.
Example #1
You can evaluate some simple molecule properties returning a single number by evaluating the following Chemical Terms functions, one-by-one:
ringCount()aromaticRingCount()chainAtomCount()smallestRingSize()bondCount()mass()You can find all available functions in the structure based calculations reference tables. For command line access, run Chemical Terms Evaluator by simply typing:
evaluate -e "ringCount()" aroms.smilesand you will get the number of rings for each input molecule:
1
1
1
1
1
1
3
2
1
1
1
1
1
1
You can print the results of the other evaluations in the same way.
Example #2
There are other functions that compute a single numeric value for the input molecule, e.g.
avgPol()logp()psa()These functions compute the average molecular polarizability component based on the 3D geometry, the logP and the topological polar surface area, respectively.
The corresponding Chemical Terms command line example is e.g.
evaluate -e "psa()" aroms.smiles, which gives the following results:
0
17.07
45.82
0
0
0
0
15.79
20.23
20.23
26.02
26.02
29.1
0
Example #3
Some (atomic) plugin calculations - when called for the molecule as a whole - return an array containing the calculation result for each atom:
charge()pka()energyE()polarizability()
The Chemical Terms Evaluator example in this case can be e.g.:
evaluate -e "energyE()" aroms.smilesIn the result the array elements are separated by ';' characters, and invalid values (NaN, not-a-number values) are returned when there is no result calculated for the atom; in case of energyE() these are the non-aromatic atoms, represented by empty strings:
2.54;2.54;2.54;2.54;2.54;2.54
;0.5;3.78;1.57;1.05;0.99;1.21;0.99;1.05
1.73;-0.02;1.73;0.7;0.29;0.19;0.3;0.19;0.29
1.84;2.77;2.27;2.54;2.31;2.54;2.27
3.03;2.57;2.51;2.54;2.51;2.54;2.51
3.03;2.57;2.48;2.54;2.48;2.57;3.03;2.48
2.42;2.42;2.23;3.03;2.01;3.03;2.23;2.42;2.42;2.23;3.03;2.01;3.03;2.23
3.88;3.87;3.76;4.31;3.99;3.85;3.43;4.33;3.74
4.2;1.73;1.45;1.56;1.46;1.56;1.45
4.02;2.24;1.77;1.26;1.55;1.3;1.55;1.26
1.55;3.09;1.98;2.55;2.06;2.55;1.98
;2.29;1.07;2.26;1.8;2.05;1.83;2.05;1.8
;0.82;4.12;3.1;1.83;1.2;1.42;1.25;1.42;1.2
2.54;2.54;2.54;2.54;2.54;2.54
To perform the plugin calculation for specific atom(s) you should specify the corresponding atom index list as parameter(s):
charge(0)pka(0, 1)energyE(2, 3, 4)polarizability(2)
Example #4
You can also pass other, plugin-specific parameters, e.g. you can compute acidic pKa values for each atom or for specified atoms by:
pka('acidic')pka(0, 2, 3, 'acidic')Another typical structure-based calculation parameter is the pH. For some plugin calculations if the pH is specified, the plugin calculates with the physiological microspecies of the input molecule at the given pH, e.g.
charge('7.4')charge('7.4', 0)energyE('6.5', 2, 3)psa('9.4')Note that the pH value is always enclosed in quotes, while atom indices are specified as integers, e.g. typing
evaluate -e "psa('9.4')" aroms.smilesgives the following:
0
17.07
45.82
0
0
0
0
15.79
20.23
20.23
26.02
27.64
29.1
0
,which differs from the results received for the input molecule itself for two molecules (compare with the non-parameterized PSA calculation example above).
For logD the pH value simply means the pH where the logD is to be taken, e.g.
logd('7.4')
Example #5
Another specific building block of chemical expressions is the set of substructure search functions. Currently we have two such functions:
-
match() tests substructure matching and returns true or false depending on the search result.
-
matchCount() counts the search hits and returns this numerical result.
Both functions have the same parametrization:
-
the target molecule (by default, this is the input molecule)
-
optional target atom indices to be matched
-
the query molecule (mandatory)
-
optional query maps to be matched
You can find a summary on the usage of these match functions in the Match Reference Tables. For example, to test whether the input molecule contains an oxygen or a sulphur atom with a single hydrogen type:
match('[O,S;H1]')To count these atoms, write
matchCount('[O,S;H1]')Now to match and find a nitrogen, aliphatic or aromatic atom with at least one attached hydrogen, type:
match('[#7][H]')matchCount('[#7][H]')Chemical Terms Evaluator example in this case is:
evaluate -e "match('[#7][H]')" aroms.smilesThe result is:
0
0
0
0
0
0
0
1
0
0
1
1
1
0
Note that true is treated and displayed as a numerical 1 and false as a numerical 0. This is useful when you test a rule like bioavailability, where you require that at least a certain number of the specified conditions be satisfied.
Example #6
You can use the -x, --extract <format> option to filter out from the input and output precisely those molecules which satisfy the boolean expression:
evaluate -e "match('[#7][H]')" -x smiles aroms.smilesThe result is:
c1ccc2[nH]ccc2c1
Nc1ccccc1
CC(N)c1ccccc1
CC(=O)Nc1ccccc1
To test atom-by-atom matches you should refer to a target atom by its atom index (0-based) and possibly one or more query maps. For example
match(2, '[#8]C=O')will test whether target atom 2 is part of a carboxylic group, while
match(2, '[#8:1]C=[O:2]', 1)will test whether target atom 2 is a carboxylic OH, and
match(2, '[#8:1]C=[O:2]', 1, 2)will test whether target atom 2 is a carboxylic oxygen.
Note that the target atom index should be written in front of the query, while the query atom map(s) should follow the query. However, in most cases the target atom is not specified by explicitely writing an atom index, since we do not know the atom order in the target. Instead, the target atom usually comes from another context, such as ratom(i) or patom(i) from a reaction context or else a superior function iterates through all atoms and collects those that satisfy the match condition. The most typical example for such a function is the filter() function explained below.
Example #7
You can also use logical operators to include two or more substructure search results:
match('[O,S;H1]') || match('[#7][H]')will test for matching any of OH, SH OR a nitrogen with at least one attached hydrogen. In this case the command line example is simply
evaluate -e "match('[O,S;H1]') || match('[#7][H]')" aroms.smiles
The result is:
0
0
0
0
0
0
0
1
1
1
1
1
1
0
The logical AND operator can also be applied in the same way:
match('[O,S;H1]') && match('[#7][H]')will test for matching both an OH or SH AND a nitrogen with at least one attached hydrogen.
Furthermore, you can add the number of search hits to count all the above functional groups:
matchCount('[O,S;H1]') + matchCount('[#7][H]')
Example #8
The filter function takes a boolean subexpression as argument, iterates through the atoms of the input molecule and evaluates this inner subexpression for each atom. The result is an atom index array containing the atom indices satifying the inner subexpression. For example
filter("charge() > 0")returns the indices of atoms with positive partial charge. Test this with the Chemical Terms Evaluator:
evaluate -e "filter('charge() > 0')" aroms.smilesThe result is:
1
3;4;8
1
1
0;1
with empty rows meaning no positive partial charge for that molecule. You can check the charge values by simply typing:
evaluate -e "charge()" aroms.smiles
Example #9
Another typical example for an inner condition is the match() function:
filter("match('[#8:1]C=[O:2]', 1, 2)")will list all carboxylic oxygens in the input molecule, while
filter("match('[#7:1][H]', 1)")will list all nitrogen atoms with at least one attached hydrogen. To test this type:
evaluate -e "filter(\"match('[#7:1][H]', 1)\")" aroms.smilesNote that you can nest single and double quotes but if you need more than two, then you should escape the inner quotes identical to the outer quotes. To escape this problem you can save your filter in a file and switch to the -f option:
evaluate -e filter.txt aroms.smilesThe result is:
4
0
2
3
that is, there are four input molecules containing a nitrogen atom with an attached hydrogen, and all of these contain only one such atom.
Example #10
As another example, you can list aromatic carbons by:
evaluate -e "filter(\"match('c')\")" aroms.smilesThe resulting atom index arrays are displayed as comma-separated lists:
0;1;2;3;4;5
3;4;5;6;7;8
3;4;5;6;7;8
1;2;3;4;5;6
1;2;3;4;5;6
1;2;3;4;5;7
0;1;2;3;4;5;6;7;8;9;10;11;12;13
0;1;2;3;5;6;7;8
1;2;3;4;5;6
2;3;4;5;6;7
1;2;3;4;5;6
3;4;5;6;7;8
4;5;6;7;8;9
0;1;2;3;4;5
You can evaluate atomic plugin calculations on these filtered atoms, too. For example
evaluate -e "charge(filter(\"match('c')\"))" aroms.smiles will return the partial charges on aromatic carbons:
-0.06;-0.06;-0.06;-0.06;-0.06;-0.06
-0.02;-0.02;-0.05;-0.04;-0.05;-0.02
0.03;0.03;-0.03;-0.03;-0.03;0.03
-0.06;-0.07;-0.06;-0.07;-0.06;-0.07
-0.02;-0.04;-0.05;-0.06;-0.05;-0.04
-0.02;-0.03;-0.05;-0.03;-0.02;-0.01
-0.06;-0.06;-0.05;-0.04;-0.03;-0.04;-0.05;-0.06;-0.06;-0.05;-0.04;-0.03;-0.04;-0.05
-0.05;-0.05;-0.04;-0.09;-0.11;-0.04;-0.04;-0.04
-0.01;-0.06;-0.06;-0.1;-0.06;-0.06
-0.04;-0.05;-0.06;-0.06;-0.06;-0.05
-0.04;-0.07;-0.07;-0.09;-0.07;-0.07
-0.05;-0.05;-0.06;-0.06;-0.06;-0.05
-0.02;-0.04;-0.05;-0.06;-0.05;-0.04
-0.06;-0.06;-0.06;-0.06;-0.06;-0.06
You can also apply various array functions for the above results, e.g. you can take the sum of these charges by:
evaluate -e "sum(charge(filter(\"match('c')\")))" aroms.smilesThe result is:
-0.37
-0.2
-0.01
-0.39
-0.26
-0.15
-0.63
-0.47
-0.35
-0.32
-0.41
-0.33
-0.27
-0.37
Example #11
A similar expression to the exclude rule of the Friedel-Crafts acylation reaction can be:
match("[#15][H]") || (max(pka(filter("match('[O,S;H1]')"), "acidic")) > 14.5) ||(max(pka(filter("match('[#7:1][H]', 1)"), "basic")) > 0) This condition tests whether the molecule contains a phosphorus with an attached hydrogen, or the maximum acidic pKa taken on an OH or SH is greater than 14.5, or the maximum basic pKa taken on nitrogen atoms with attached hydrogen is positive.
Saying that the maximum basic pKa on certain atoms is positive is the same as saying that there should be an atom among these atoms with a positive pKa, but the former is the way to describe this fact in Chemical Terms. Thus, the above condition is satisfied if any of the following is satisfied:
-
the molecule contains a phosphorus with an attached hydrogen, or
-
the molecule contains an OH or SH with acidic pKa greater than 14.5, or
-
the molecule contains a nitrogen with positive basic pKa with an attached hydrogen
Note that in logical expressions we put simpler calculations to the front to increase efficiency: if the first simple matching rule match("[#15][H]") is passed then there is no need to evaluate the other two with more complicated filtering and pKa calculation.
To test this condition on our input molecules save the filter into a text file and type:
evaluate -e friedel-crafts-exclude.txt aroms.smilesIt turns out that the following input molecules satisfy this exclude rule, so the Friedel-Crafts acylation will not be performed for these molecules:
Example #12
Finally we test some well-known and easily expressible chemical conditions on our input molecules:
-
Lipinski's rule of five:
(mass() <= 500) &&
(logP() <= 5) &&
(donorCount() <= 5) &&
(acceptorCount() <= 10)To test this type
evaluate -e lipinski.txt aroms.smilesIt turns out that all of our input molecules satisfy Lipinski's rule.
-
Lead-likeness:
(mass() <= 450) &&
(logD("7.4") >= -4) && (logD("7.4") <= 4) &&
(ringCount() <= 4) &&
(rotatableBondCount() <= 10) &&
(donorCount() <= 5) &&
(acceptorCount() <= 8)To test this type
evaluate -e lead-likeness.txt aroms.smilesThere is one molecule that fails to satisfy this rule:
c1ccc2cc3ccccc3cc2c1
evaluate -e"logD('7.4')""c1ccc2cc3ccccc3cc2c1"The reason is that its logD at pH=7.4 is too high: 4.05.
-
Bioavailability:
(mass() <= 500) +
(logP() <= 5) +
(donorCount() <= 5) +
(acceptorCount() <= 10) +
(rotatableBondCount() <= 10) +
(PSA() <= 200) +
(fusedAromaticRingCount() <= 5) >= 6Note that summing up the 7 subresults above means to count how many of them are satisfied. The requirement that this sum should be at least 6 means that we do not require all of the subconditions to be satisfed, but instead we allow at most one of them to fail.
To test this type
evaluate -e bioavailability.txt aroms.smilesIt turns out that all of our input molecules satisfy this bioavailability rule.
-
Ghose filter:
(mass() >= 160) && (mass() <= 480) &&
(atomCount() >= 20) && (atomCount() <= 70) &&
(logP() >= -0.4) && (logP() <= 5.6) &&
(refractivity() >= 40) && (refractivity() <= 130)To test this type:
evaluate -e ghose-filter.txt aroms.smilesIt turns out that only our previous molecule failing lead-likeness passes this Ghose filter.
-
Scaffold hopping:
refmol = "c1ccccc1";
dissimilarity("ChemicalFingerprint", refmol) -
dissimilarity("PharmacophoreFingerprint", refmol) > 0.6Note that molecule constants can be defined by a molecule file path or a SMILES string. Multiple expressions are separated by ';' characters, whitespace characters can be added freely for readability, since they are not considered by the evaluation process.
This condition tests whether the chemical and the pharmacophore dissimilarities between benzene and the input molecule are sufficiently far from each other, that is, the molecules should not be reasonably similar in pharmacophoric features but distant in chemical structure.
To test this save the function in a txt file and type:
evaluate -e scaffold-hopping.txt aroms.smilesIt turns out that none of our input molecules satisfies this rule.
Note that the default output is a 0-1 list representing true-false values for each input molecule.
You can use the -x, --extract <format> option to output precisely those input molecules that satisfy the condition. For example
evaluate -e ghose-filter.txt -x smiles aroms.smileswill give the result:
c1ccc2cc3ccccc3cc2c1
Reaction rule examples
In this section we show two sample reactions:
-
Friedel-Crafts acylation
-
Baeyer-Villiger ketone oxidation
We demonstrate the use of reaction rules:
-
Reactivity rules describe the chemical conditions of the reaction, while
-
Selectivity rules select the main products and sort them by importance / occurrence in case of multiple possibilities, finally
-
Exclude rules are used to exclude products that we do not want to produce even if they may be chemically feasible (e.g. because they are not stable or the corresponding reactants are likely to produce side-reactions)
These chemical expressions formulating these rules access reaction data through a reaction context . Here are some examples for using this context:
-
reactant(0): the first reactant
-
reactant(1): the second reactant
-
product(0): the first product
-
product(1): the second product
-
ratom(1): the reactant atom matching map 1 in the reaction equation
-
ratom(3): the reactant atom matching map 3 in the reaction equation
-
patom(1): the product atom matching map 1 in the reaction equation
-
patom(2): the product atom matching map 2 in the reaction equation
You should map your reactions according to ChemAxon's reaction mapping style to access reactant and product atoms by map matching. You can also use Structure/Mapping in MarvinSketch to use automatical mapping.
Example #1
Our first example is the Friedel-Crafts acylation, an electrophilic aromatic substitution reaction with acyl halides producing oxo compounds.
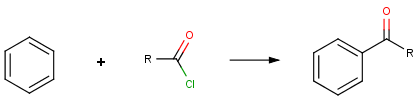
This reaction can be represented by the following scheme:
The reaction has the following rules:
-
Reactivity:
charge(ratom(1), "aromaticsystem") <= -0.2
,meaning that the aromatic system should be at least as activated as dihalobenzenes.
-
Selectivity:
-energyE(ratom(1))
This is a specific directional rule saying that the electrophilic substitution takes place on the aromatic carbon atom with the lowest localization energy having an attached electrophile in the transition state.
-
Selectivity tolerance:
0.02
With this setting we change the default tolerance 0.0001 to accept other aromatic carbons having a similar localization energy with maximum difference 0.02 from the lowest value. Results will be sorted by this localization energy in ascending order, taking lowest first.
-
Exclusion:
match(ratom(2), "[C:1]C=C", 1) || match(reactant(0), "[O,S]C=[O,S]") || match(reactant(0), "P[H]") || (max(pka(reactant(0), filter(reactant(0), "match('[O,S;H]')"), "acidic")) > 14.5) || (max(pka(reactant(0), filter(reactant(0), "match('[#7][H]')"), "basic")) > 0)
The first reactant may not contain carboxylic acid group or its thio analogue. Exclude acryloyc halides as acylating agent. Exclude PH compounds, and aromatic compounds containing such nucleophilic groups wich can be acylated among these conditions (OH, SH compounds with higher pKa than 14.5, and NH compounds with higher pKb than 0). This is a more complicated, somewhat heuristical rule. You may want to have a look at a similar condition in the basic examples section referring to a molecule context. Note, that now our condition should explicitly refer to the input molecule as reactant(0), meaning the first reactant, while in a molecule context the expression implicitly refers to the input molecule.We exclude reactant pairs satisfying any of the following subexpressions ( || means logical OR ):
-
The second reactant is an acryloic halide, testing this with an atom-matching condition on carbon atoms:
match(ratom(2), "[C:1]C=C", 1)
-
The first reactant contains a phosphorus with an attached hydrogen:
match(reactant(0), "P[H]") -
The first reactant contains an OH or SH with acidic pKa greater than 14.5:
max(pka(reactant(0), filter(reactant(0), "match('[O,S;H]')"), "acidic")) > 14.5 -
The first reactant contains a nitrogen with positive basic pKa with an attached hydrogen:
max(pka(reactant(0), filter(reactant(0), "match('[#7][H]')"), "basic")) > 0
Note that we put simpler conditions first to increase efficiency. In the last two subexpressions, we use the filter function with a match filtering conditi to extract the relevant atoms for the pKa calculation. Finally, we take max of these values to test whether any of them exceeds a certain limit.
-
Refer to the Chemical Terms Reference Tables for ChemAxon's Chemical Terms function/plugin calculation calculation syntax summary and explanation.
Now it is time to process this reaction on some reactants. We will process the reaction on 14 reactant pairs.
Our reactant file for the first reactant contains a set of aromatic molecules stored in a SMILES file:

The second reactant set is very simple - we take the same acid-halide for each of the aromatic molecules above:
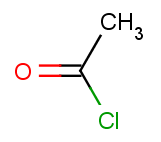
Then we will test benzene with another acid-halide as well:
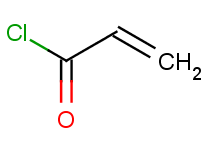
Now run the Reactor to process the reaction. The second reactants are stored in a SMILES file with all but one molecule being identical to the first acid-halide above, while the last one being the second one:
react -r Friedel-Crafts_acylation.mrv aroms.smiles acidhalides.smiles -t reaction -o Friedel-Crafts_results.smilesThe resulted reactions are stored in a result SMILES file.
To analyze the results examine the reactant pairs one-by-one. Observe that the only rule referring the second reactant is the exclude rule stating that the acid-halide carbon should not be the acryloic-halide mapped carbon. It follows that our first acid-halide, acetyl chloride is not excluded but our second acid halide, acryloyl chloride, obviously satisfies this condition and therefore the last reactant pair with benzene paired with this second acid-halide is excluded from the result. Now in the analyzation below, we examine the first reactant.
You can check the reactivity and selectivity rules with
evaluate -e "charge('aromaticsystem')" r1.smilesevaluate -e "energyE()" r1.smileswhere r1.smiles is a first reactant in SMILES form. These commands will list the evaluation results for each atom, seperated by ';' characters (the results are copied under the command):
-
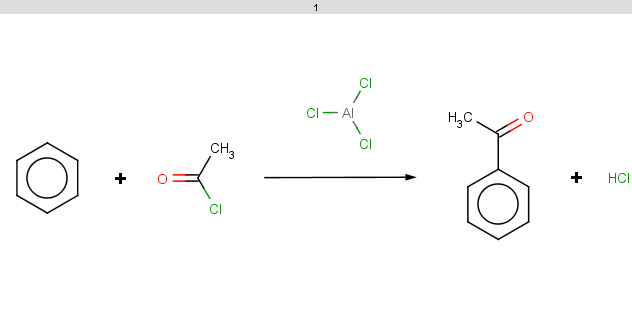
benzene satisfies the reactivity condition (sum of partial pi charges in the aromatic system).
evaluate -e "charge('aromaticsystem')" "c1ccccc1"-0.37;-0.37;-0.37;-0.37;-0.37;-0.37
However, it does not satisfy the exclude condition since it does not contain phosphorus or ionizable atoms (no pKa values), therefore the reaction is processed and the result is:
Observe that the selectivity rule does not play here since it evaluates to the same value because of molecule symmetry. -
Our second aromatic molecule (acetophenone) will not react because it fails to satisfy the reactivity rule:
evaluate -p 3 -e "charge('aromaticsystem')" "CC(=O)c1ccccc1"0;0;0;-0.199;-0.199;-0.199;-0.199;-0.199;-0.199
Now we see that the condition is not satisfied (-0.199 > -0.2).
-
The third reactant (nitrobenzene) will not react for the same reason:
evaluate -e "charge('aromaticsystem')" "O=N(=O)c1ccccc1"0;0;0;-0.01;-0.01;-0.01;-0.01;-0.01;-0.01
-
Toluol (reactant #4) satisfies the reactivity rule:
evaluate -e "charge('aromaticsystem')" "Cc1ccccc1"0;-0.39;-0.39;-0.39;-0.39;-0.39;-0.39
Toluol is obviously not excluded (for the same reason as benzene), therefore we should evaluate the selectivity rule to determine the main products:
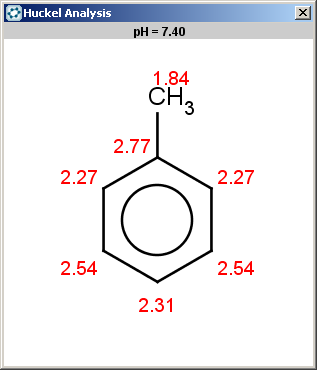
Since our selectivity rule says to take the minimal localization energy (the localization energy is multiplied by -1 to reverse the result order, that is to take the minimum instead of maximum), the ortho position is the best; the para position is also accepted because the corresponding value is within tolerance: 2.46-2.45 < 0.02 .
The resulting reaction is therefore:
-
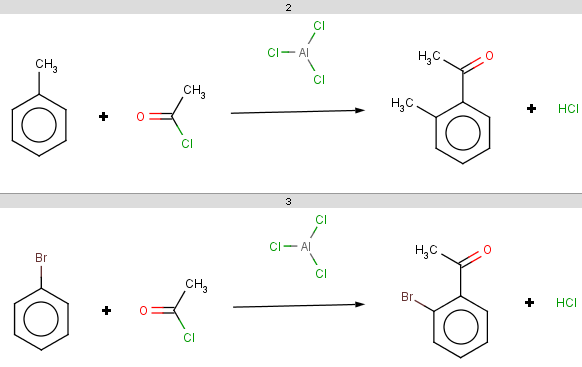
For bromobenzene the situation is the same as with toluol:
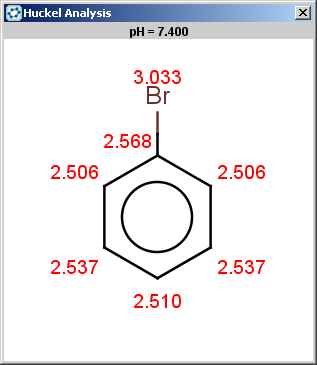
The ortho and para positions are accepted, with the ortho position being the main result:
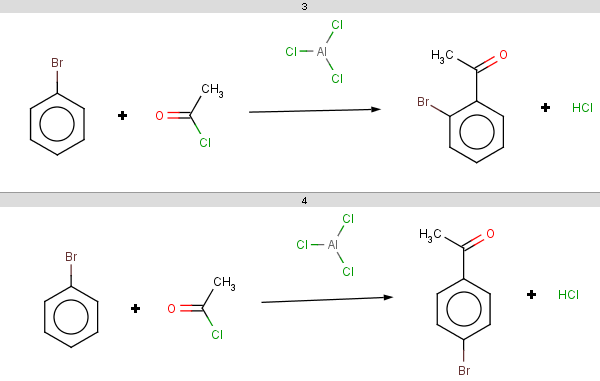
-
For anthracene the reactivity rule is satisfied:
evaluate -e "charge('aromaticsystem')" "c1ccc2cc3ccccc3cc2c1"-0.63;-0.63;-0.63;-0.63;-0.63;-0.63;-0.63;-0.63;-0.63;-0.63;-0.63;-0.63;-0.63;-0.63
Anthracene is not excluded for the same reasons as toluol and benzene and the selectivity rule now determines a single position:
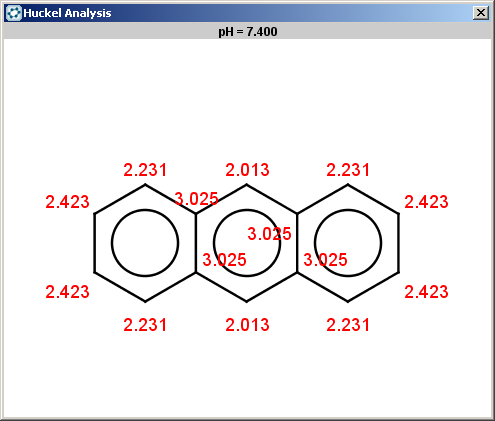
The reaction result is shown below:
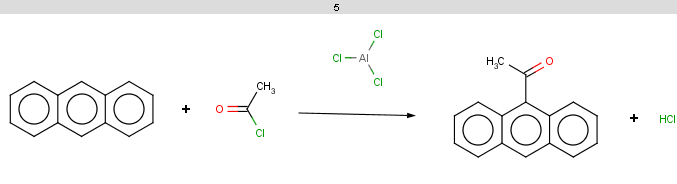
-
For indole the reactivity rule is satisfied:
evaluate -e "charge('aromaticsystem')" "c1ccc2[nH]ccc2c1"-0.55;-0.55;-0.55;-0.55;-0.55;-0.55;-0.55;-0.55;-0.55
Indole is not excluded because there is no basic pKa on its nitrogen atom:
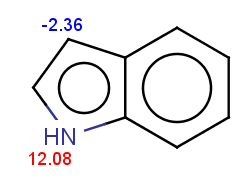
The selectivity rule selects a single position for reaction: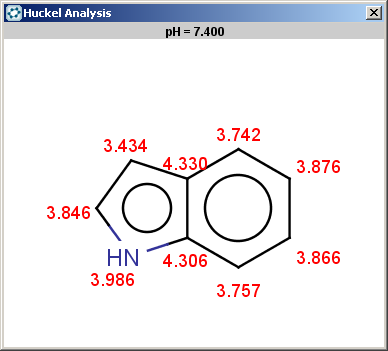
The reaction result is shown below:
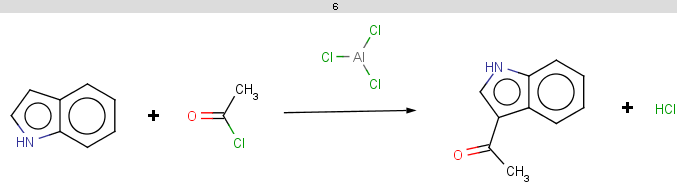
-
The reactivity rule for phenol is satisfied:
evaluate -e "charge('aromaticsystem')" "Oc1ccccc1"0;-0.35;-0.35;-0.35;-0.35;-0.35;-0.35
Phenol is not excluded, because the acidic pKa of its OH group is not greater than the specified 14.5 limit:
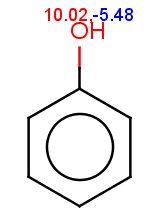
The selectivity rule selects the ortho and the para positions: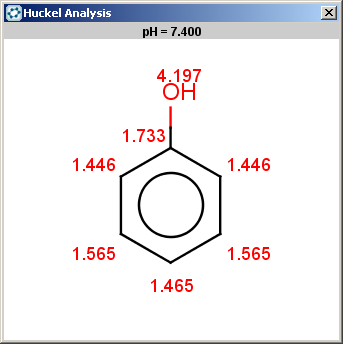
The resulting reactions are shown below:
-
The next three molecules satisfy the exclude condition regarding the conditions on the pKa values (positive basic pKa on a nitrogen having an attached H or acidic pKa greater than 14.5 on an OH or SH):
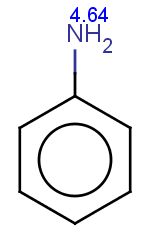
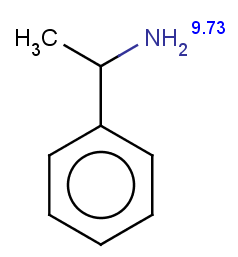
-
Acetanilide has negative pKa on its nitrogen, therefore it is not excluded:
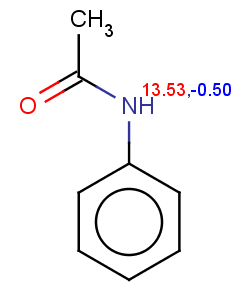
evaluate -e "charge('aromaticsystem')" "CC(=O)Nc1ccccc1"Phenylacetamide satisfies the reactivity rule:
0;0;0;0;-0.27;-0.27;-0.27;-0.27;-0.27;-0.27
The selectivity rule selects a single position (ortho):
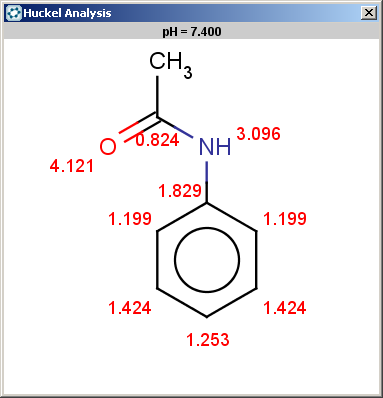
The resulting reaction is shown below:
Example #2
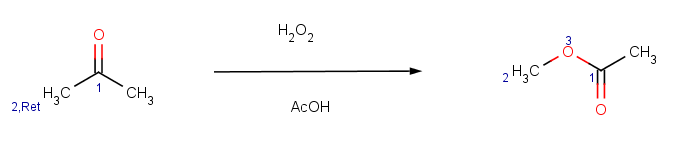
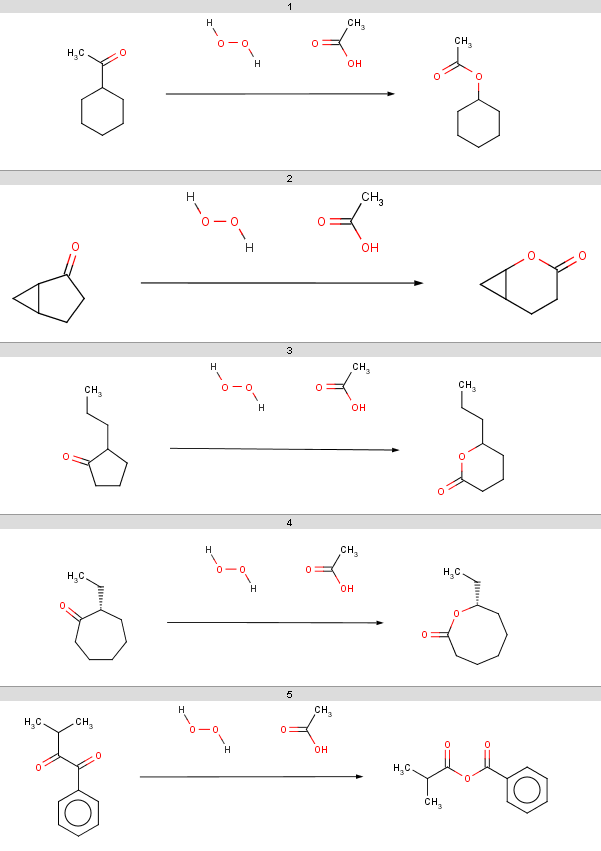
Our second example is the Baeyer-Villiger ketone oxidation, a ketone oxidation to an ester upon treatment with peroxy acids.

The reaction can be represented by the following scheme:
|
|
The reaction has the following rules:
-
Reactivity:
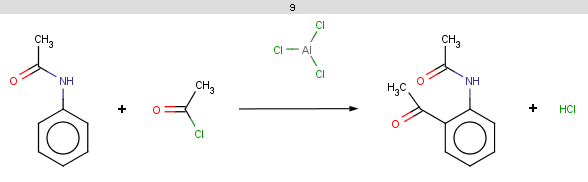
!match(ratom(1), "O=[C:1][C]([H])C=O", 1)
This means that β-diketones are able to enolize do not react; we test this by an atom mathching condition: the ketone carbon matching map 1 in the reaction equation should not match the carbon with map 1 in beta-diketones:
-
Selectivity:
charge(ratom(2), "sigma")
This means that the oxygen goes between the carbonyl carbon and its neighbour with the biggest σ charge.
-
Selectivity tolerance: we do not set the tolerance, therefore the default tolerance 0.0001 will be applied, which practically means that only the main product is accepted.
-
Exclude:
match(reactant(0), "[#5,#7,#8,#14,#15,#16][H]") ||
match(reactant(0), "[n,s]") ||
match(reactant(0), "[#6]S[#6,#16]") ||
match(reactant(0), "[#6]S([#6])=[N,O]") ||
match(reactant(0), "[H]C=O")We exclude reagents containing BH, NH, OH, SiH, PH or SH groups or aromatic N, S or sulfide, disulfide, sulfoxyde or sulfimide groups and we also exclude aldehydes producing carboxylic acids with these reagents.
Refer to the Chemical Terms Reference Tables for ChemAxon's Chemical Terms function/plugin calculation syntax summary and explanation.
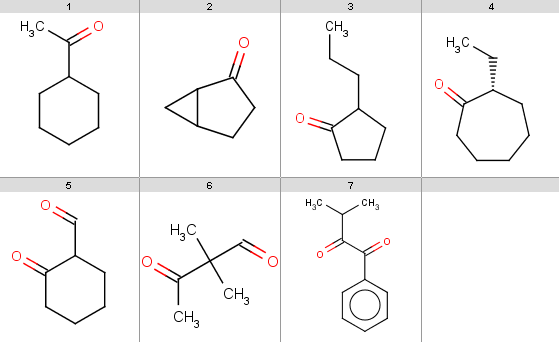
Our reactant file is contains the following 7 molecules:
Now run Reactor to process the reaction:
react -r Baeyer-Villiger_ketone_oxidation.mrv ketones.smiles -t reaction -o Baeyer-Villiger_results.smilesThe result reactions are stored in Baeyer-Villiger_results.smiles:
|
|
You should note, that our 5th ketone does not react because it is a β-diketone and hence does not satisfy our reactivity criteria. The 6th ketone is an α-diketone matching [H]C=O in our exclude rule, therefore that will not react either. The specific chemical reason is that these ketones produce anhydrides instead of undergoing oxidation.
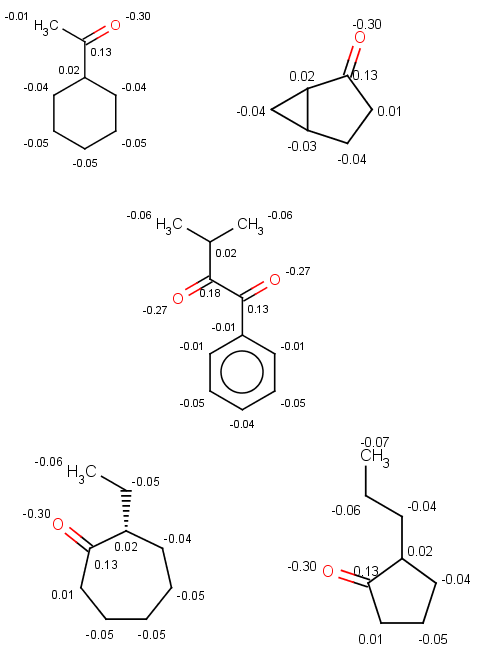
All other ketones from our input set react (satisfy our reactivity rule and are not excluded by our exclude rule), therefore our selectivity rule will determine the main product. We show the atomic sigma-charges below, look at the charge values on atoms matching reaction map 2 , marked with 2 in the following sample:
|
|
Now look at these sigma-charge values and check that the bigger value is selected in our results above:
|
|
Search filtering examples
In this section we show some examples for search filters. These expressions filter targets, queries and/or search hits: the substructure search is performed only for target-query pairs satisfying the filtering condition, furthermore, search hits are filtered by the expression.
Search data (target, query, search hits) is accessed through a search context. Here are some examples for using this context:
-
target() or mol(): the target molecule, this is usually omitted since the default input molecule is the target
-
query(): the query molecule
-
m(1): query atom index of query atom with map 1
-
m(2): query atom index of query atom with map 2
-
h(0) or hit(0): target atom index matching query atom with atom index 0 (0-based indexing)
-
h(3) or hit(3): target atom index matching query atom with atom index 3 (0-based indexing)
-
hm(2): target atom index matching query atom with map 2
-
hm(4): target atom index matching query atom with map 4
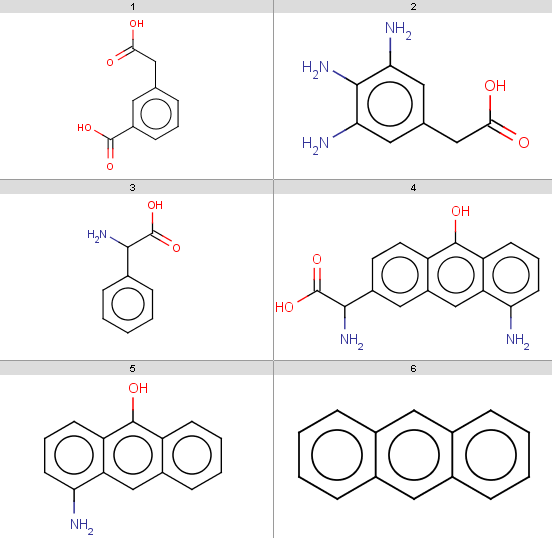
In the examples below, the target molecules are stored in targets.smiles:
|
|
Queries are stored in queries.smarts:
|
|
In the following examples we use the jcsearch command line tool to perform substructure search with filtering:
-
Filtering targets:
-
Output targets with carboxylic group(s) having molecular mass bigger than 170:
jcsearch targets.smiles -q "[#8:1]C=O" -e "mass() > 170"OC(=O)Cc1cccc(c1)C(O)=O
Nc1cc(CC(O)=O)cc(N)c1N
NC(C(O)=O)c1ccc2c(O)c3cccc(N)c3cc2c1Note that our 3rd target molecule also contains a carboxylic group but is not present in the output since it has molecular mass 151.16. You can check molecular masses by:
evaluate -e "mass()" targets.smiles180.16
181.19
151.16
282.29
209.24
178.23 -
Add another restriction on the ring count, and you will filter out the 4th target too:
jcsearch targets.smiles -q "[#8:1]C=O" -e "mass() > 170 && ringCount() == 1"OC(=O)Cc1cccc(c1)C(O)=O
Nc1cc(CC(O)=O)cc(N)c1N -
You can also filter by some well-known chemical rules, such as Lipinski's rule of five, Lead-likeness, Bioavailability or the Ghose filter, and any booleancondition shown in the basic examples section above, since here the input molecule will automatically refer to the target. For example, test the Ghose filter with the carboxylic group query:
jcsearch targets.smiles -q "[#8:1]C=O" -e ghose-filter.txtOC(=O)Cc1cccc(c1)C(O)=O
Only the first target is accepted because only our first 4 targets contain a carboxylic group and only the first of these satisfied the Ghose filter:
evaluate -e ghose-filter.txt targets.smiles1
0
0
0
1
1
-
-
Filtering queries:
-
First set a molecular mass requirement on the query:
jcsearch targets.smiles -q "[#8:1]C=O" -e "mass(query()) > 20"OC(=O)Cc1cccc(c1)C(O)=O
Nc1cc(CC(O)=O)cc(N)c1N
NC(C(O)=O)c1ccccc1
NC(C(O)=O)c1ccc2c(O)c3cccc(N)c3cc2c1All target molecules containing carboxylic group(s) are returned, since our query satisfies has molecular mass 44.01:
evaluate -e "mass()" "[#8:1]C=O"44.01
However, when running this with our nitrogen query then there is no output, although we have 4 target molecules containing nitrogen:
jcsearch targets.smiles -q "[#7:1]" -e "mass(query()) > 20"because nitrogen has molecular mass 14.01:
evaluate -e "mass()" "[#7:1]"14.01
-
Next, set a condition on a query atom. In this example we require that the query atom with map 1 should have partial charge greater than -0.05. This time we have empty result set for the carboxylic group but have 4 search hits for the nitrogen:
jcsearch targets.smiles -q "[#8:1]C=O" -e "charge(query(), m(1)) > -0.05"jcsearch targets.smiles -q "[#7:1]" -e "charge(query(), m(1)) > -0.05"Nc1cc(CC(O)=O)cc(N)c1N
NC(C(O)=O)c1ccccc1
NC(C(O)=O)c1ccc2c(O)c3cccc(N)c3cc2c1
Nc1cccc2c(O)c3ccccc3cc12since the nitrogen has zero charge while the partial charge on the carboxylic OH is -0.1. Note, that we refer to the query molecule as query() and its mapped atom with atom map 1 as m(1). You can also refer to query aotms by atom indices but in most cases it is more difficult to determine. However, since nitrogen is only one atom, you can safely write:
jcsearch targets.smiles -q "[#7]" -e "charge(query(), 0) > -0.1"Nc1cc(CC(O)=O)cc(N)c1N
NC(C(O)=O)c1ccccc1
NC(C(O)=O)c1ccc2c(O)c3cccc(N)c3cc2c1
Nc1cccc2c(O)c3ccccc3cc12You can also omit the atom map in the query.
-
-
Filtering search hits:
In these examples we filter search hits by setting conditions on pKa values calculated on target atoms matching carboxylic oxygens or nitrogens. In order to check the results easily we show the pKa values together with atom indices for the target molecules:
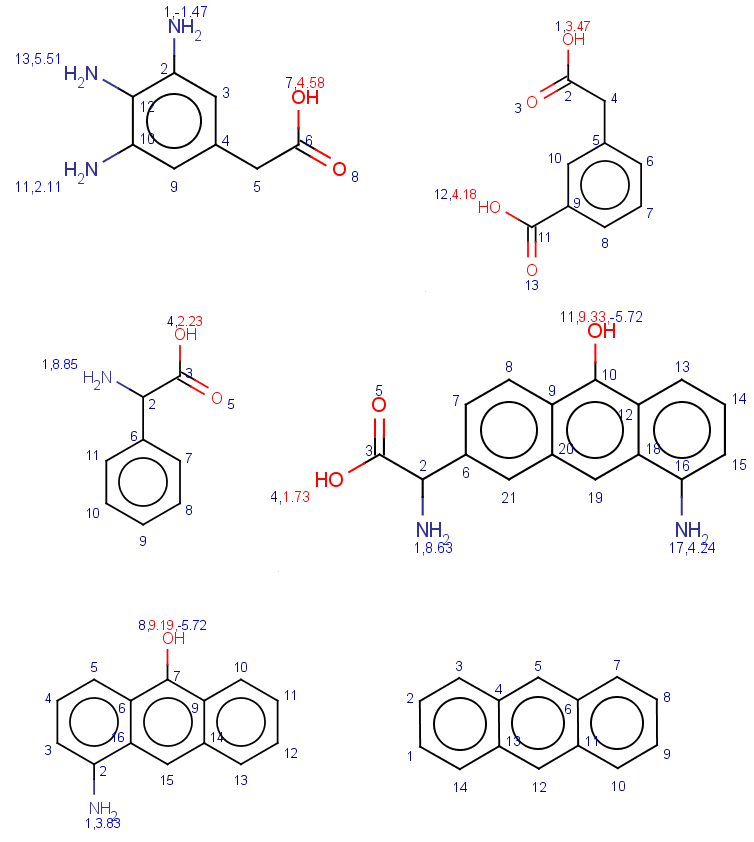
-
First look at all carboxylic group hits and all nitrogen hits:
jcsearch targets.smiles -q "[#8:1]C=O" --allHitsQuery 0 matches:
Match 0:[ 1, 2, 3 ]
Match 1:[ 12, 11, 13 ]
OC(=O)Cc1cccc(c1)C(O)=O
Query 0 matches:
Match 0:[ 7, 6, 8 ]
Nc1cc(CC(O)=O)cc(N)c1N
Query 0 matches:
Match 0:[ 4, 3, 5 ]
NC(C(O)=O)c1ccccc1
Query 0 matches:
Match 0:[ 4, 3, 5 ]
NC(C(O)=O)c1ccc2c(O)c3cccc(N)c3cc2c1
jcsearch targets.smiles -q "[#7:1]" --allHitsQuery 0 matches:
Match 0:[ 1 ]
Match 1:[ 11 ]
Match 2:[ 13 ]
Nc1cc(CC(O)=O)cc(N)c1N
Query 0 matches:
Match 0:[ 1 ]
NC(C(O)=O)c1ccccc1
Query 0 matches:
Match 0:[ 1 ]
Match 1:[ 17 ]
NC(C(O)=O)c1ccc2c(O)c3cccc(N)c3cc2c1
Query 0 matches:
Match 0:[ 1 ]
Nc1cccc2c(O)c3ccccc3cc12 -
Next set filtering condition on the pKa at target atom matching query atom with map 1, which is either the carboxylic OH or the nitrogen depending on the query. Note that we refer to this atom as hm(1):
jcsearch targets.smiles -q "[#8:1]C=O" --allHits -e "pka(hm(1)) > 4"Query 0 matches:
Match 0:[ 12, 11, 13 ]
OC(=O)Cc1cccc(c1)C(O)=O
Query 0 matches:
Match 0:[ 7, 6, 8 ]
Nc1cc(CC(O)=O)cc(N)c1NCheck these results by looking at the pKa values.
jcsearch targets.smiles -q "[#7:1]" --allHits -e "pka(hm(1)) > 4"Query 0 matches:
Match 0:[ 13 ]
Nc1cc(CC(O)=O)cc(N)c1N
Query 0 matches:
Match 0:[ 1 ]
NC(C(O)=O)c1ccccc1
Query 0 matches:
Match 0:[ 1 ]
NC(C(O)=O)c1ccc2c(O)c3cccc(N)c3cc2c1 -
Finally combine hit filtering with a condition on the target molecule:
jcsearch targets.smiles -q "[#8:1]C=O" --allHits -e "mass() > 170 && ringCount() == 1 && pka(hm(1)) > 4"
Query 0 matches:
Match 0:[ 12, 11, 13 ]
OC(=O)Cc1cccc(c1)C(O)=O
Query 0 matches:
Match 0:[ 7, 6, 8 ]
Nc1cc(CC(O)=O)cc(N)c1Njcsearch targets.smiles -q "[#7:1]" --allHits -e "mass() > 170 && ringCount() == 1 && pka(hm(1)) > 4"Query 0 matches:
Match 0:[ 13 ]
Nc1cc(CC(O)=O)cc(N)c1NNote that both carboxylic hits are kept because these targets satisfy both conditions, while two nitrogen hits are filtered out, because one target fails to satisfy the mass condition, and the other one has 3 rings. Observe that we put simpler conditions to the front for efficiency: if the mass condition fails, then the others are not considered at all.
-